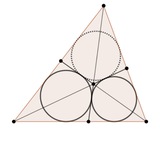
Теорема Клера-Блисса
Через середины сторон треугольника проведены три синие параллельные прямые. Докажите, что прямые, симметричные сторонам относительно соответствующих синих прямых, пересекаются в одной точке. Найдите геометрическое место точек пересечения.
Ничего не значащий спойлер:
If we call the Minkowski perpendicular bisector of a segment with slope a the line through its midpoint with slope 1/a (the two lines are orthogonal in the Minkowski metric), the Klehr-Bliss theorem says that the Minkowski perpendicular bisectors of the three sides of a triangle are concurrent. The proof follows the usual proof: any point on the Minkowski perpendicular bisector of a segment is Minkowski equidistant from the two ends.
Через середины сторон треугольника проведены три синие параллельные прямые. Докажите, что прямые, симметричные сторонам относительно соответствующих синих прямых, пересекаются в одной точке. Найдите геометрическое место точек пересечения.
Ничего не значащий спойлер:
November 28, 2024
Forwarded from Непрерывное математическое образование
https://geometry.ru/olimp/2025/2025_zaoch_rus.pdf
https://geometry.ru/olimp/2025/2025_zaoch_eng.pdf
начинается заочный тур XXI олимпиады им. И.Ф.Шарыгина
как обычно: 24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
https://geometry.ru/olimp/2025/2025_zaoch_eng.pdf
начинается заочный тур XXI олимпиады им. И.Ф.Шарыгина
как обычно: 24 задачи по классической геометрии для разных классов, в основном непростые, русская и англ. версии
December 1, 2024
Через центр O описанной окружности треугольника ABC проведена прямая, пересекающая стороны AB, BC и CA в точках F, D и E соответственно. Докажите, что окружности, построенные на AD, BE и CF как на диаметрах пересекаются в двух точках, одна из которых лежит на описанной окружности треугольника ABC, а вторая на окружности девяти точек.
December 2, 2024
December 3, 2024
December 3, 2024
December 4, 2024
December 5, 2024
Олимпиадная геометрия
1912.07566.pdf
Китайские коллеги продолжают традицию брать на олимпиады задачи по комбинаторной геометрии из статей. На этот раз взяли на всекитайскую национальную олимпиаду 2025 взяли вот такую задачу.
December 6, 2024
December 11, 2024
December 12, 2024
Forwarded from Dima Shvetsov
Кажется, что некоторое представление о Сергее и его вкусах в математике можно получить по такой замечательной лекции:
https://www.mathnet.ru/present50
https://www.mathnet.ru/present50
December 12, 2024
Про параболическую точку Фейербаха не очень понимаю я кое-что...
Само утверждение такое: если парабола вписана в треугольник, то парабола с тем же направлением оси, проходящая через середины сторон, касается первой.
Доказать это можно по-разному. Можно, во-первых, применить какие-то общие соображения, видимо. Во-вторых, можно, видимо, переписать доказательство со счетом углов в общем виде, пригодном для углов в параболе. Ну и, наконец, можно просто посчитать.
Так вот если посчитать... то окажется, что точка касания имеет ту же абсциссу, что и центр масс треугольника (считаем, что параболы вертикальны) . И вот это мне не понятно... Есть ли у этого какая-то интерпретация, в частности, для окружностей?
Само утверждение такое: если парабола вписана в треугольник, то парабола с тем же направлением оси, проходящая через середины сторон, касается первой.
Доказать это можно по-разному. Можно, во-первых, применить какие-то общие соображения, видимо. Во-вторых, можно, видимо, переписать доказательство со счетом углов в общем виде, пригодном для углов в параболе. Ну и, наконец, можно просто посчитать.
Так вот если посчитать... то окажется, что точка касания имеет ту же абсциссу, что и центр масс треугольника (считаем, что параболы вертикальны) . И вот это мне не понятно... Есть ли у этого какая-то интерпретация, в частности, для окружностей?
December 15, 2024
У геометрической олимпиады им. Ясинского появился свой красивый сайт
https://yasinskyi-geometry-olympiad.com/en/home-eng/
https://yasinskyi-geometry-olympiad.com/en/home-eng/
December 20, 2024
December 21, 2024
Как показывают ответы выше, вопрос не такой уж и интуитивно понятный. На самом деле, если пытаться не просто угадать, а доказать соответствующий факт, то задача становится еще запутаннее.
Я знаю общий ответ в n-мерном пространстве и доказательство, в котором первый шаг... это преобразование Фурье характеристической функции куба. Правда, не выглядит тривиально?
Тем не менее, если ответ получен, то вместе с ним получается и ответ на такой вопрос.
Вопрос. Предположим в R^n даны два выпуклых центрально-симметриченых тела K и L с центром симметрии в начале координат. Оказалось, что любое центральное (n-1)-мерное сечение K имеет площадь меньше, чем сечение L той же гиперплоскостью. Верно ли, что тогда объем K меньше объема L?
Ответ оказывается отрицательным и контрпримером в размерностях больше 10 (не помню точно) служат куб и шар. А все потому, что можно явно указать сечение наибольшей площади у куба и посчитать ее.
Естественным продолжением служит такой вопрос.
Вопрос. Предположим в R^n даны два выпуклых центрально-симметриченых тела K и L с центром симметрии в начале координат. Оказалось, что любое центральное (n-1)-мерное сечение K имеет площадь как минимум в C раз меньше, чем сечение L той же гиперплоскостью. Верно ли, что существует такая универсальная константа C (не зависящая от размерности), которая гарантирует, что объем K меньше объема L?
Этот вопрос оставался открытым около 40 лет. И позавчера опубликовали препринт, подтверждающий, что это утверждение верно!
Что интересно, у этой гипотезы (теперь уже теоремы) есть множество абсолютно разнородных и нетривиальных переформулировок. Помню я даже как-то делал доклад в лаборатории Ч и рассказывал про это.
Вот, например, simplex conjecture (не помню, эквивалентна ли, но в одну сторону следствие точно есть).
Simplex conjecture. Обозначим через m(K) среднее значение объемов симплексов, лежащих внутри K. Тогда среди всех выпуклых тел единичного объема максимум m достигается на симплексе. (Минимум, кстати, достигается на шаре и это известно.)
Я знаю общий ответ в n-мерном пространстве и доказательство, в котором первый шаг... это преобразование Фурье характеристической функции куба. Правда, не выглядит тривиально?
Тем не менее, если ответ получен, то вместе с ним получается и ответ на такой вопрос.
Вопрос. Предположим в R^n даны два выпуклых центрально-симметриченых тела K и L с центром симметрии в начале координат. Оказалось, что любое центральное (n-1)-мерное сечение K имеет площадь меньше, чем сечение L той же гиперплоскостью. Верно ли, что тогда объем K меньше объема L?
Ответ оказывается отрицательным и контрпримером в размерностях больше 10 (не помню точно) служат куб и шар. А все потому, что можно явно указать сечение наибольшей площади у куба и посчитать ее.
Естественным продолжением служит такой вопрос.
Вопрос. Предположим в R^n даны два выпуклых центрально-симметриченых тела K и L с центром симметрии в начале координат. Оказалось, что любое центральное (n-1)-мерное сечение K имеет площадь как минимум в C раз меньше, чем сечение L той же гиперплоскостью. Верно ли, что существует такая универсальная константа C (не зависящая от размерности), которая гарантирует, что объем K меньше объема L?
Этот вопрос оставался открытым около 40 лет. И позавчера опубликовали препринт, подтверждающий, что это утверждение верно!
Что интересно, у этой гипотезы (теперь уже теоремы) есть множество абсолютно разнородных и нетривиальных переформулировок. Помню я даже как-то делал доклад в лаборатории Ч и рассказывал про это.
Вот, например, simplex conjecture (не помню, эквивалентна ли, но в одну сторону следствие точно есть).
Simplex conjecture. Обозначим через m(K) среднее значение объемов симплексов, лежащих внутри K. Тогда среди всех выпуклых тел единичного объема максимум m достигается на симплексе. (Минимум, кстати, достигается на шаре и это известно.)
December 21, 2024
Про сечения единичного куба (то, что их площадь не превосходит sqrt(2)) можно прочитать маленькую заметку вот тут. Если вы знаете более простое решение, то обязательно напишите мне!))
December 21, 2024
December 23, 2024
Forwarded from Математические кружки | «МТ кружки»
Примерно через месяц будут проходить региональные олимпиады по математике. Поэтому мы, команда преподавателей «МТ кружков», как и в прошлом году, хотим предложить попробовать вам свои силы в прорешивании тренировочных олимпиад!
Ниже — подробности.
Тренировочные варианты будут составлены "с нуля". Для их составления мы будем использовать задачи из различных источников (например, просмотрим олимпиады других стран). При этом задачи не будут "гуглиться", а сами варианты по сложности и композиции будут похожи на классические варианты региональных олимпиад ВсОШ и Эйлера.
Среди преподавателей «МТ кружков» есть 4 экс-тренера сборной Москвы по математике (Меньщиков А.Б., Бахарев Ф.Л., Афризонов Д.В. и Попов Л.А.), а также действующий тренер сборной Санкт-Петербурга по математике (Смирнов А.В.).
Про нашу команду преподавателей вы можете почитать, например, вот тут. Нашей общей экспертизы с запасом хватит для составления!
Первый вариант будет опубликован 6 января (понедельник), а его разбор будет опубликован 11 января (суббота).
Второй вариант будет опубликован 13 января (понедельник), а его разбор будет опубликован 18 января (суббота).
Третий вариант будет опубликован 20 января (понедельник), а его разбор будет опубликован 25 января (суббота).
Все варианты и ссылки на все стримы с разборами будут опубликованы в нашем канале.
Для всех желающих мы готовы организовать проверку письменных решений наших тренировочных вариантов. В качестве обратной связи мы не просто сообщим баллы по каждой задаче, но и напишем подробные комментарии по оформлению.
Стоимость проверки решений по всем трём вариантам составляет 2700 руб. Если вас это интересует, то заполните, пожалуйста, эту короткую анкету.
Подписаться на «Математические кружки»
Please open Telegram to view this post
VIEW IN TELEGRAM
December 23, 2024
This media is not supported in your browser
VIEW IN TELEGRAM
Bulgaria MO, 1999, Problem 2
На картинке два подобных треугольника. O и H — центр описанной окружности и ортоцентр маленького, H' — ортоцентр большого. Докажите, что OH=OH'.
На картинке два подобных треугольника. O и H — центр описанной окружности и ортоцентр маленького, H' — ортоцентр большого. Докажите, что OH=OH'.
December 24, 2024
Forwarded from Geometry Ukraine (Matthew Kurskyi)
YGO 2024, 8 клас, Задача 2.
Нехай 𝐼 та 𝑂 — центри вписаного та описаного кіл трикутника 𝐴𝐵𝐶. Точки 𝑃 та 𝑄 такі, що 𝐴𝐼𝑂𝑃 та 𝐵𝐼𝑂𝑄 — рівнобічні трапеції (𝐴𝐼||𝑂𝑃, 𝐵𝐼||𝑂𝑄). Доведіть, що 𝐶𝑃 = 𝐶𝑄.
Володимир Брайман
Нехай 𝐼 та 𝑂 — центри вписаного та описаного кіл трикутника 𝐴𝐵𝐶. Точки 𝑃 та 𝑄 такі, що 𝐴𝐼𝑂𝑃 та 𝐵𝐼𝑂𝑄 — рівнобічні трапеції (𝐴𝐼||𝑂𝑃, 𝐵𝐼||𝑂𝑄). Доведіть, що 𝐶𝑃 = 𝐶𝑄.
Володимир Брайман
December 24, 2024